Sorry if my question is a little more mathematical in nature, but my question is:
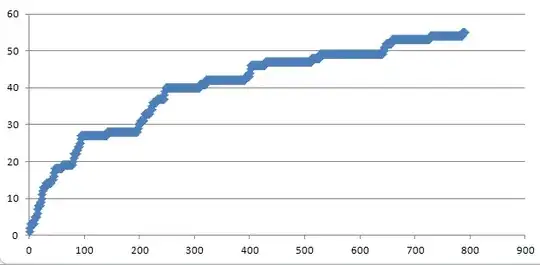
Suppose I took a document of some length whether it be news article, book, or something of that sort. What sort of relationship would I expect between the document's length and the number of unique words contained in it.
There are two constraints a graph would contain: the line y = x meaning every word I read is unique and the line y = |english| where we recognize that English has a finite number of words, or some sort of upper bound although I don't want to get into a discussion on how many words are in the English language.
Perhaps more practically, how long a document on average would I need to retrieve to get a list of 100 unique English words, 1000 unique English words , or some other value? This of course would differ between languages, but I am interested in English.