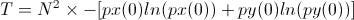6

Is there a measure for the rate of language drift? In one answer to this question, it was suggested that drift had slowed for technological reasons, but may also be speeding up because of different technologies.

How is this slowing determined? I would imagine statistically?

Is there a unit of measurement for language drift?

Community
  • 1
Sam
  • 161
  • 1
  • So in the linked thread, they're talking about the rate at which spelling changes. But that's pretty arbitrary, and it often has more to do with politics than with linguistics. (Think of all the central Asian languages that have switched between the Arabic, Cyrillic and Roman alphabets -- pretty much at the whim of whoever was in charge.) Are you interested in how spelling evolves, or in how the actual spoken language evolves? – Leah Velleman Nov 09 '11 at 00:20
  • 1
    I'd like to expand on Dan's answer to point out that writing systems are not languages, but merely arbitrary, consciously-designed sets of symbols for representing languages. Sorry, that's a hobby-horse I beat a lot as I think this conflation of 'language' and 'spelling/writing system' causes a lot of misunderstanding. – Gaston Ümlaut Nov 09 '11 at 03:51
  • Well, I didn't mean that to be an "answer" so much as an honest request for clarification. "How do you measure the rate at which spelling changes?" would be a perfectly valid question, if that's what Sam meant to ask. – Leah Velleman Nov 10 '11 at 18:25
  • 1
    @DanVelleman, yes. Language drift, which I recognize as different from spelling, but spelling provides, at least, some metric for change. Trying to quantify change in sounds, seems much, much more difficult, although not, perhaps impossible. That's generally the point of the question. – Sam Nov 11 '11 at 17:00

1 Answers1

2

I don't know of a standard method, but it shouldn't be too difficult to make some metric of the variation in an orthographic form.

We'll use the Wright-Fisher model, which is used to model genetic drift in biology. Let's say that a word has orthographic variants x and y, and their prevalences at time t = 0 are px(0) and py(0) = 1 – px(t). Imagine that all of the tokens of our word belong in generation 0. Now we start to do a procedure like this:

  1. Select N words at random from generation 0, using the prevalences at t = 0
  2. Now the words that we have selected form generation 1, which has its own prevalences, px(1) and 1 – px(1).
  3. Select N words from generation 1 to create generation 2, and so on, until we get to generation n where either px(n) = 0 or px(n) = 1. At this point we can say that one variant of the word has fixed, and there is no more drift.

A way of measuring how much longer the system is going to drift is by calculating the mean fixation time, or the average number of generations from generation 0 that it takes for one variant to fix. For large N, this number is:

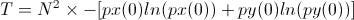
enter image description here

Since we set N arbitrarily, the important term is the one with the logarithms in it, which is equivalent to the entropy of the system, though the choice of base is e rather than 2. So if I were starting from scratch, I'd take the entropy as a way of quantifying the present variability, and the amount of time remaining before the system stabilizes, as a baseline measure.

Just a thought.

Principles of Evolution eds. H Meyer-Ortmanns and S. Thurner (Springer, 2011).

Otavio Macedo
  • 8,208
  • 5
  • 45
  • 110
  • This sounds promising, but I'm looking for actual methodologies and measures (if they exist) for drift. – Sam Nov 11 '11 at 17:02